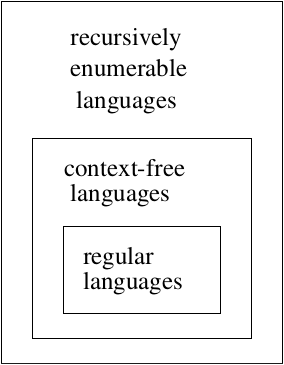
What is the set of languages that TM's accept? We know that they accept RL's and CFL's. And additional languages.
Question: Is there any language that a TM cannot accept?
Definition: A language \(L\) is recursively enumerable if there exists a TM \(M\) such that \(L = L(M)\) .
[Hah! All that says is that the languages that a TM can deal with now have a name!]

We say that \(M\) accepts the language. For every \(w\) in \(L\) , \(M\) should accept \(w\) .
Question: What happens if \(w\) is not in \(L\) ? Saying that \(M\) can properly accepting strings in \(L\) doesn't define happens if \(w\) is not in \(L\) . \(M\) may not halt in that case.
Note: We do not get a yes or no answer, just a yes if w is in L!
Definition: A language \(L\) is recursive if there exists a TM \(M\) such that \(L = L(M)\) and \(M\) halts on every \(w \in \Sigma^+\) . Thus, A language \(L\) is recursive if and only if there exists a membership algorithm for it.
[Note the difference beteen a recursive language (one that is recognized by a TM) and a recursive algorithm (which merely means that it calls itself).]
NOTE: We will ignore the empty string. In Chapter 9, the definition of the TM assumes that the input string is always padded on both sides of the input. If the input could be a blank, the tape head would not know where the input string was. It would be easy to adjust the definition to include the empty string, but for now we will just examine languages that do not include \(\lambda\) .
Not a problem if we use a one-sided tape as our base definition, which is a good argument for doing it that way.
To enumerate all \(w \in \Sigma^+\) in a recursive language \(L\) :